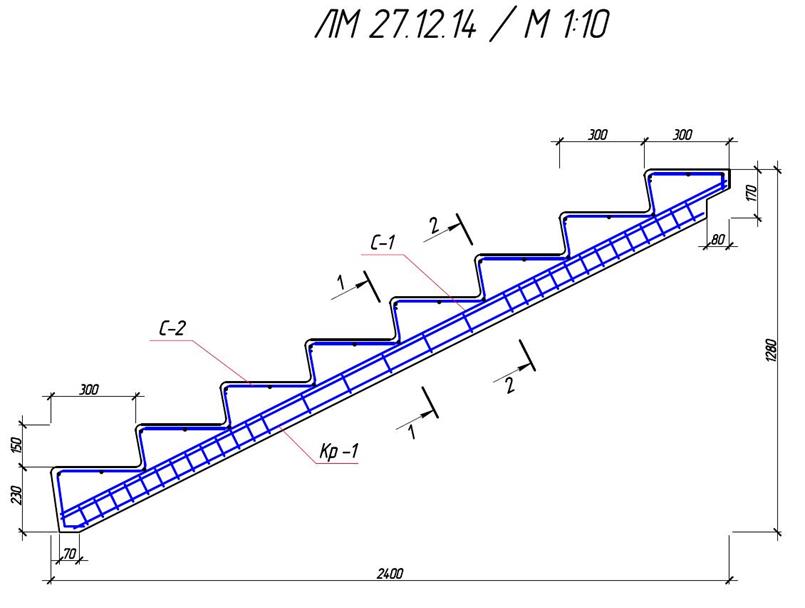
Расчет сборного железобетонного марша
 Железобетонный марш шириной 1,1 м для лестницы жилого здания.
Железобетонный марш шириной 1,1 м для лестницы жилого здания.
Высота этажа 3.0м.
Угол наклона марша 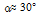 , ступени размером
, ступени размером 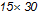 .
.
Бетон класса В25 с расчетными характеристиками:
Rb = 1,45кН/см2; Rbt = 0,105кН/см2; Rb.ser = 1,85кН/см2; Rbt.ser=0,16 кН/см; 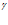 b2=0,9.
b2=0,9.
При изготовлении конструкции примем естественное твердение бетона Eb=3,0´103 кН/см2.
Арматура каркасов класса А300: Rs=28 кН/см2; Es=20´103кН/см2; для сеток арматура класса В500: Rs=37,5 кН/см2; Es=17´103 кН/см2.
Нормативное значение временной нагрузки 3 кН/м2.
Коэффициент надежности по назначению здания 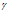 n=0,95.
n=0,95.
Сбор нагрузок на лестничный марш и определение внутренних усилий в сечениях элемента от внешней нагрузки
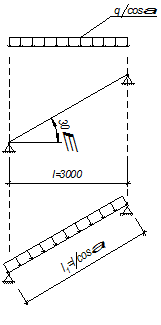
Расчетная схема
Собственный вес лестничного марша по каталогу сборных железобетонных конструкций для жилищного строительства: 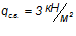 .
.
Временная нормативная нагрузка для лестниц жилого дома: 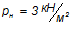 .
.
Коэффициент надежности по нагрузке: 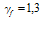 .
.
Расчетная нагрузка на 1 м марша:
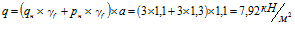 .
.
Расчетный изгибающий момент в середине пролета марша:
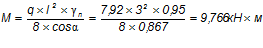 .
.
Поперечная сила на опоре:
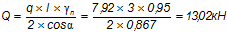 .
.
Расчет прочности по нормальным сечениям
Применительно к типовым заводским формам назначим толщину плиты 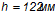 , ширину
, ширину 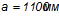 .
.
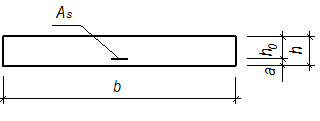
Расчетный участок плиты
Толщина защитного слоя бетона: 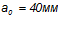 .
.
Расчетная высота сечения: 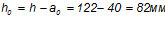 .
.
Коэффициент:
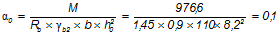 .
.
Относительная высота сжатой зоны:
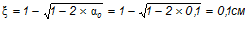 .
.
Площадь сечения арматуры:
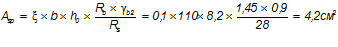
Примем 4Æ12 А300 с As = 4,52 см2.
Расчет прочности по наклонным сечениям
Проверим выполнение условий:
1) 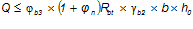
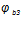 — коэффициент, учитывающий влияние вида бетона, принимаемый: для тяжелого бетона —
— коэффициент, учитывающий влияние вида бетона, принимаемый: для тяжелого бетона — 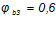 ;
;
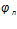 — коэффициент, учитывающий влияния продольной силы, т.к. лестничный марш проектируется без предварительного обжатия, то
— коэффициент, учитывающий влияния продольной силы, т.к. лестничный марш проектируется без предварительного обжатия, то 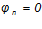 .
.
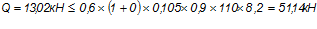
2) 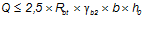
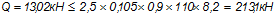
3) 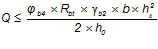
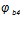 — коэффициент, принимаемый для тяжелого бетона
— коэффициент, принимаемый для тяжелого бетона 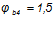
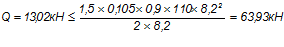 .
.
Условия выполняется, прочность наклонных сечений обеспечена.
Поперечные стержни каркаса устанавливаем из конструктивных соображений с шагом 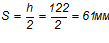 .
.
Примем шаг стержней 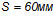 . В середине пролета шаг поперечных стержней
. В середине пролета шаг поперечных стержней 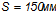 .
.
Фактическая длина марша 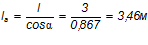
Определение геометрических характеристик сечения
Коэффициент, равный отношению модулей упругости двух материалов:
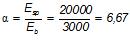
Площадь приведенного сечения составит:
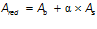
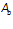 — площадь сечения бетона:
— площадь сечения бетона:
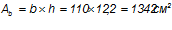
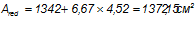
Статический момент приведенного сечения относительно оси I-I, проходящей по нижней грани сечения:
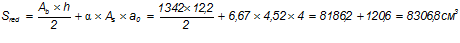
Расстояние от центра тяжести сечения до наиболее растянутой грани (до оси I-I):
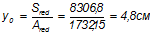
Расстояние от центра тяжести сечения до наиболее сжатой грани (до оси II-II):
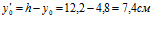
Момент инерции сечения относительно оси, проходящей через центр тяжести данного сечения:
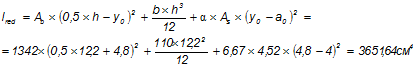
Момент сопротивления относительно оси I-I:
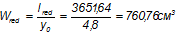
Момент сопротивления приведенного сечения относительно оси II-II:
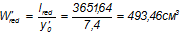
Расчет по трещиностойкости
Проверим выполнение условия
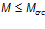
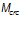 — момент внутренних усилий, воспринимаемый сечением, перед образованием трещин:
— момент внутренних усилий, воспринимаемый сечением, перед образованием трещин:
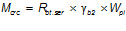
Пластический момент сопротивления сечения:
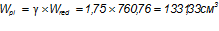
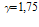 — безразмерный коэффициент.
— безразмерный коэффициент.
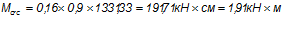
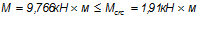
Условие не выполняется, необходим расчет по раскрытию трещин.
Расчет на раскрытие трещин
Расчет сводится к проверке условия:
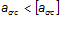

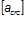 — предельно допустимая ширина раскрытия трещин, обеспечивающая сохранность арматуры;
— предельно допустимая ширина раскрытия трещин, обеспечивающая сохранность арматуры;
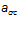 — ширина раскрытия трещин:
— ширина раскрытия трещин:
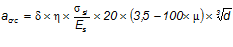
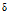 — коэффициент, принимаемый для изгибаемых и внецентренно сжатых элементов
— коэффициент, принимаемый для изгибаемых и внецентренно сжатых элементов 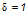 ;
;
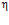 — коэффициент, принимаемый при стержневой арматуре периодического профиля
— коэффициент, принимаемый при стержневой арматуре периодического профиля 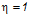
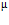 — коэффициент армирования сечения:
— коэффициент армирования сечения:
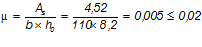
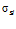 — приращение напряжений от действия внешней нагрузки:
— приращение напряжений от действия внешней нагрузки:
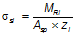 .
.
Момент от постоянных нагрузок:
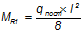
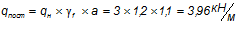
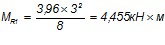
Момент от полной нормативной нагрузки:
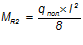
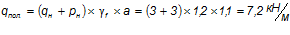
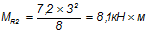
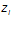 — расстояние от центра тяжести площади сечения растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной:
— расстояние от центра тяжести площади сечения растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне сечения над трещиной:
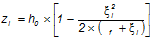
 — относительная высота сжатой зоны бетона:
— относительная высота сжатой зоны бетона:
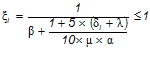
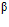 — коэффициент, принимаемый для тяжелого и легкого бетона
— коэффициент, принимаемый для тяжелого и легкого бетона 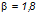 ;
;
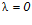 ;
;
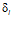 — коэффициент, принимаемый по формуле:
— коэффициент, принимаемый по формуле:
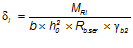
при постоянных нагрузках:
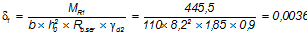
при полных нагрузках:
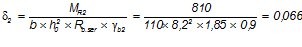
Тогда при постоянных нагрузках:
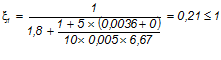
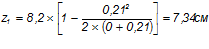
при полных нагрузках:
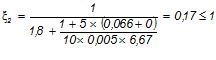
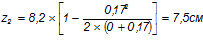
Приращение напряжений:
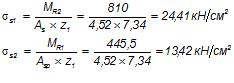
Тогда
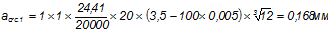
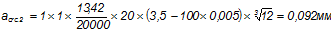
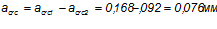 <
<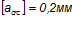
Условия выполняются, ширина раскрытия трещин не превышает предельно допустимой величины.
Расчет по деформациям
Расчет сводится к проверке условия:
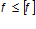
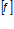 — предельно допустимый прогиб элемента;
— предельно допустимый прогиб элемента; 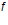 — прогиб элемента:
— прогиб элемента:
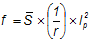
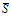 — коэффициент, зависящий от расчетной схемы и вида нагрузки: при равномерно распределенной нагрузке —
— коэффициент, зависящий от расчетной схемы и вида нагрузки: при равномерно распределенной нагрузке — 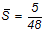
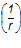 — полная кривизна изгибаемого элемента;
— полная кривизна изгибаемого элемента;
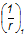 — кривизна от действия временной расчетной нагрузки:
— кривизна от действия временной расчетной нагрузки:
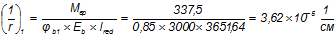
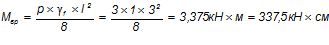
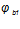 — коэффициент, учитывающий влияние кратковременной ползучести бетона, принимаемый для тяжелого бетона
— коэффициент, учитывающий влияние кратковременной ползучести бетона, принимаемый для тяжелого бетона 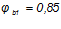 .
.
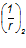 — кривизна от действия постоянной нагрузки:
— кривизна от действия постоянной нагрузки:
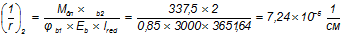
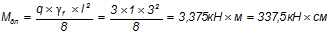
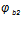 — коэффициент, учитывающий длительности ползучести бетона, принимаемый для тяжелого бетона
— коэффициент, учитывающий длительности ползучести бетона, принимаемый для тяжелого бетона 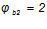 .
.
Общая кривизна:
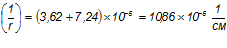
Прогиб марша:
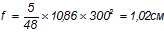 <
<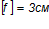 .
.
Условие выполняется, жесткость элемента
обеспечена.