Закон Гука

Портрет Роберта Гука, современная реконструкция по описаниям его коллег, 2006

Роберт Гук (англ. Robert Hooke; Роберт Хук, 18 (28) июля 1635, остров Уайт, Англия — 3 марта 1703, в Лондоне) — английский естествоиспытатель и изобретатель. Член Лондонского королевского общества (1663).

Гука сегодня называют одним из отцов физики, в особенности экспериментальной, во многих других науках ему принадлежат зачастую одни из первых основополагающих работ и множество открытий.

Закон Гука — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Открыт Робертом Гуком в 1660 году.

Закон Гука связывает такие явления, как напряжение и деформацию твердого тела, модуль силы упругости и удлинение. Модуль силы упругости, возникающей при деформации тела, пропорционален его удлинению. Удлинением называется характеристика деформативности материала, оцениваемая по увеличению длины образца из этого материала при растяжении.

Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. Напряжение — это мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий.

Деформация — изменение взаимного положения частиц тела, связанное с их перемещением друг относительно друга. Эти понятия связаны так называемым коэффициентом жесткости. Он зависит от упругих свойств материала и размеров тела.

Формулировка закона — сила упругости прямо пропорциональна деформации, т.е. сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации.

Следует иметь в виду, что закон Гука выполняется только при малых деформациях. При превышении предела пропорциональности связь между напряжениями и деформациями становится нелинейной. Для многих сред закон Гука неприменим даже при малых деформациях.

Для тонкого растяжимого стержня закон Гука имеет вид:

Здесь F сила натяжения стержня, Δl — его удлинение(сжатие), а k называется коэффициентом упругости (или жёсткостью). Минус в уравнении указывает на то, что сила натяжения всегда направлена в сторону, противоположную деформации.

Если ввести относительное удлинение

инормальное напряжение в поперечном сечении

то закон Гука запишется так

В такой форме он справедлив для любых малых объёмов вещества.

В общем случае напряжения и деформации являются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга C_ijkl и содержит 81 коэффициент. Вследствие симметрии тензора C_ijkl, а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

где σ_ij — тензор напряжений, —тензор деформаций. Для изотропного материала тензор C_ijkl содержит только два независимых коэффициента.

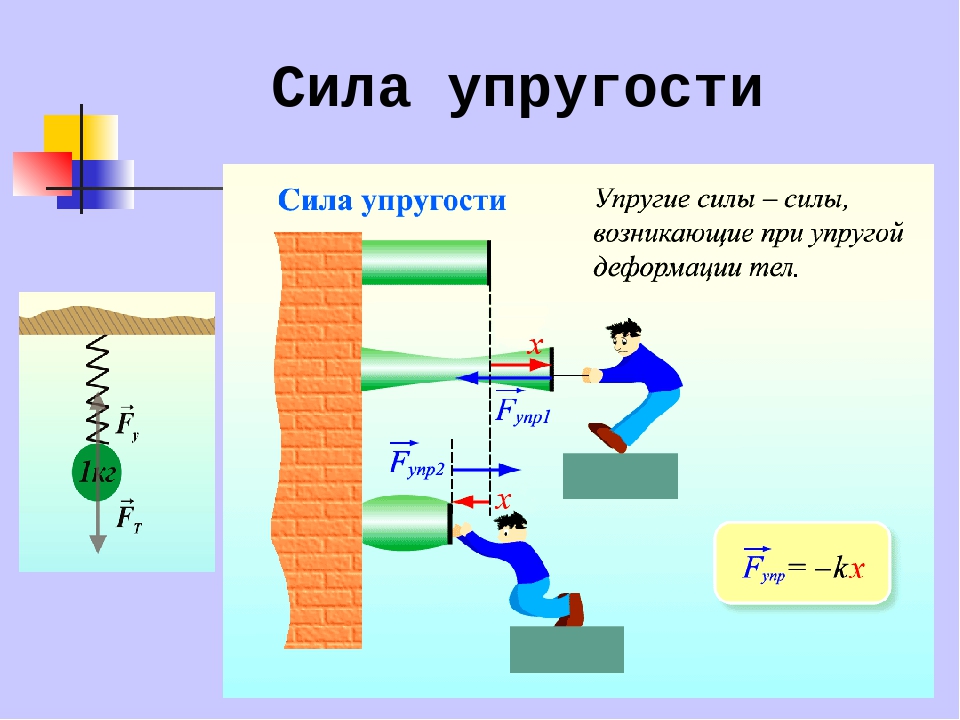
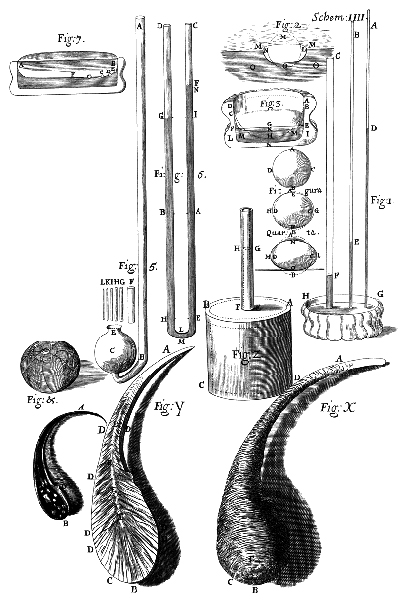
Иллюстрация из «Микрографии» посвящена капиллярным явлениям и воздушным пузырькам

Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.

Сила упругости возникает при деформации, и направлена она на восстановление первоначальных форм и размеров строго перпендикулярно к деформируемой поверхности. У сил упругости также есть ряд особенностей.

они возникают во время деформации;
они появляются у двух деформируемых тел одновременно;
они находятся перпендикулярно поверхности, по отношению к которой тело деформируется.
они противоположны по направлению смещению частиц тела.

Упругие свойства различных тел Гук изучал в течение почти 20 лет. Упругость газов была исследована им вместе с Бойлем, результатом был труд Бойля «Новые эксперименты, касающиеся воздушной пружины», опубликованный в 1660 г., в котором Бойль пишет, что закономерность, называемую в наше время законом Бойля–Мариотта, заметил его «английский друг». Позже Гук вернется к теме упругости воздуха в «Микрографии».

Гук показал, что некоторые сорта дерева обладают хорошими упругими свойствами. Установка Гука используется и в наше время для демонстрации передечи импульса при соударения шаров.

Гук подвесил деревянные шарики на веревке так, чтобы они касались друг друга. Если ударить крайним правым шариком по двум другим, правый шар остановится, а поднимется крайний левый. В этом эксперименте можно увеличивать количество шариков – результат будет тот же. Импульс первого шарика будет без изменения передан последнему.

Для объяснения достаточно рассмотреть столкновение двух шариков, один из которых неподвижен, в системе центра масс шаров.

В этой системе шарики движутся навстречу друг другу с одинаковыми скоростями и с такими же скоростями, только противоположно направленными, разлетаются после столкновения. Перейдя в лабораторную систему координат, получим, что первый шарик полностью отдает скорость второму.

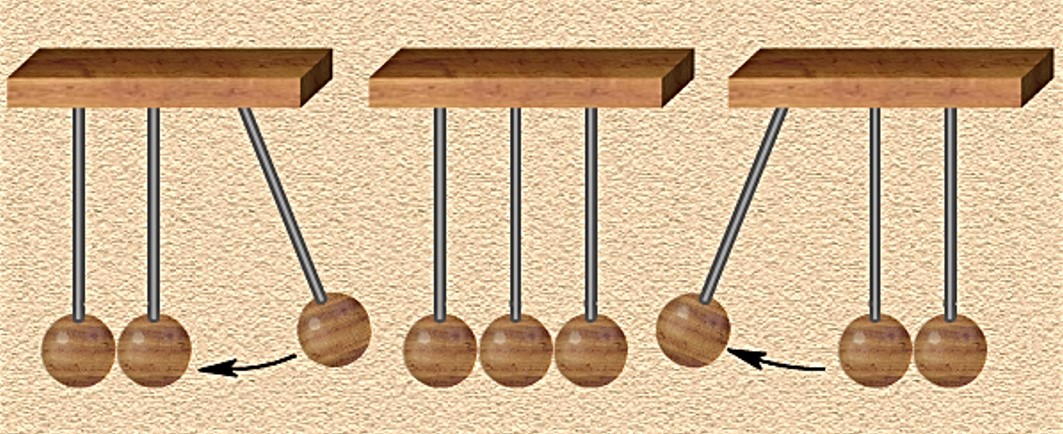
Демонстрация упругости дерева

Гук на протяжении всей жизни постоянно возвращался к исследованию темы упругости. Он исследовал свободное падение в разных средах и нашел, что тело не будет ускоряться бесконечно, а достигнет некоторой равновесной скорости. На этом принципе работал изобретенный Гуком прибор для измерения глубины реки.

Страница рукописи Гука

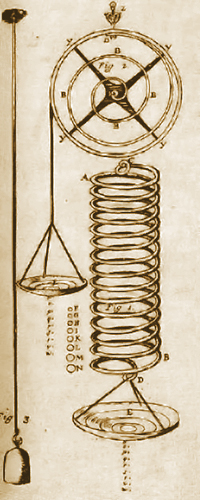
Опыты Гука. Исследование упругости пружин и струны

Основные результаты опытов по исследованию упругости тел Гук изложил в сочинении «Лекции о восстановительной способности или об упругости», вышедшим в 1678 году. По признанию автора, результаты, приведенные им в этом труде, были получены почти за 20 лет до их публикации.

Опыты, в ходе которых Гук проверял свой вывод о том, что сила упругости пропорциональна удлинению (а это, как известно, и есть закон Гука), по признанию самого Гука, такие же простые, как и сам вывод. Их можно разделить на несколько групп.

В опытах первой группы Гук использовал металлические пружины различной длины, которые изготавливал, наматывая стальную или латунную проволоку на тело цилиндрической формы. Концы пружин экспериментатор сворачивал в петли, за одну из которых подвешивал пружину, а ко второй привешивал грузы. Последовательно прикрепляя к пружине грузы равной массы, можно было наблюдать, как каждый раз пружина растягивается на одну и ту же длину.

Вторую группу опытов Гук проводил со спиральными часовыми пружинами. Спиральная пружина встраивалась в легкий латунный обод. Внешний конец пружины крепился к внутренней поверхности обода, а внутренний конец – к неподвижной оси, укрепленной в стальной рамке.

На внешнюю поверхность обода ученый наматывал тонкую нить, к свисающему концу которой крепилась легкая чашка для перегрузков. Кроме того, на обод крепилась легкая стрелка, по которой можно было судить об угле поворота обода.

Гук, последовательно помещал в чашку несколько достаточно легких перегрузков (использовались грузы массой в одну драхму каждый, 1 драхма ≈ 1,772 г) и каждый раз фиксировал угол, на который поворачивался обод. В результате стало очевидно, что при добавлении грузов равной массы обод поворачивался (а значит, спиральная пружина закручивалась) на одинаковые углы.

В третьей группе опытов Гук использовал достаточно длинные металлические струны (длина проволоки в разных опытах составляла от 20 до 40 футов,1 фут = 30,48 см). Струна растягивалась при последовательном подвешивании к ней грузов равной массы, аналогично тому, как это делалось в первой группе опытов с пружинами. Результаты получились такими же: при добавлении грузов одинаковой массы удлинения струны были одинаковыми.

Однако с позиций сегодняшнего дня мы должны указать границы применимости закона Гука: этот закон действует при условии, что деформации малы по сравнению с размерами тела.

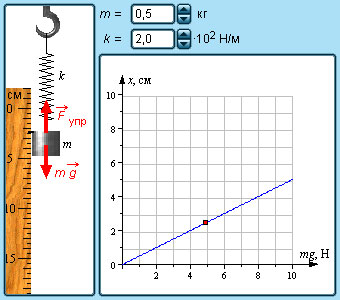
Модель 1. Закон Гука

Кроме описанных опытов с металлическими пружинами и струнами, Гук исследовал упругие свойства других тел, например, деревянных пластин. Чтобы представить себе, как проходили эти опыты, можно взять деревянную линейку, прижать рукой и удерживать один ее конец у края поверхности стола таким образом, чтобы большая часть линейки выходила за пределы стола. Несильно нажимая на свободный конец деревянной линейки, мы можем ощутить действие силы упругости, возникающей в линейке при деформации. Гук писал о том, что при деформациях изгиба внутренняя часть пластины сжимается, внешняя – растягивается, а некоторая часть в центре пластины остается в практически свободном состоянии.

Деформация тонкой пластины

В итоге своего сочинения Гук делает вывод о том, что прямая пропорцинальность силы упругости и растяжения является универсальным законом. Исследования проводились, в первую очередь, для военных целей: «При помощи этого принципа легко можно будет подсчитать различные силы луков, будут ли они сделаны из дерева, стали, рога, из сухожилий или шнуров, а также катапульт или баллист».

В качестве гражданского применения закона предлагалось использовать закономерность при создании пружинных механизмов: «Из этих же принципов будет легко вычислять силы пружины для механизма часов и соответственно приспособления механизма к пружине для того, чтобы он обеспечивал движение часов всегда с одинаковой силой». Действительно, кроме многочисленных приборов, использующих упругие силы, Гуку принадлежит авторство анкерного часового механизма, до сих пор являющегося основой механических часов. А из приборов, задуманных Гуком, интересны «механические мускулы», с помощью которых человек должен был полететь, – механизм, в котором газ, расширяющийся при нагревании и сужающийся при охлаждении, передвигает крылья.

Итак, в ходе многочисленных экспериментов установлена зависимость между нагрузкой, приложенной к стержню, и перемещениями сечений, к которым эта нагрузка приложена:

(1),

где ∆ℓ – абсолютное удлинение стержня, ℓ – длина этого стержня, А – площадь сечения стержня, Е – модуль упругости первого рода (модуль Юнга),характеризует жесткость материала, то есть способность материала сопротивляться действию внешних сил, чем жестче материал, тем меньше он деформируется при данной величине напряжений.

Размерность Е — [МПа]. Для каждого из материалов величина модуля упругости имеет свое значение: сталь, Е = 2^.10⁵ МПа, медь, Е = 1^.10⁵ МПа, алюминий, Е = 0,7^.10⁵ МПа. Значение модуля упругости устанавливается экспериментально.

Модуль продольной упругости материала (Юнга)

Для различных материалов

Произведение ЕА – называется жесткостью сечения стержня при растяжении – сжатии.

Учитывая, что F/А = σ, выражение (1) можно записать так: В этой формуле поделим левую и правую части на ℓ , тогда в правой части длины ℓ сократятся, а в левой получим:

получаем величину относительной продольной деформации.

Тогда: Или, собственно, закон Гука при растяжении-сжатии:

Динамометр

Закон был опубликован только в 1678 г., после смерти Роберта Гука. В 1680 г. этот же закон независимо от Гука открыл французский ученый Мариотт.

Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.

В общем случае напряжения и деформации описываются тензорами второго ранга в трёхмерном пространстве (имеют по 9 компонент). Связывающий их тензор упругих постоянных является тензором четвёртого ранга $C_{{ijkl}}$ и содержит 81 коэффициент. Вследствие симметрии тензора $C_{{ijkl}}$ , а также тензоров напряжений и деформаций, независимыми являются только 21 постоянная. Закон Гука выглядит следующим образом:

sigma _{{ij}}=sum _{{kl}}C_{{ijkl}}cdot varepsilon _{{kl}},

где $sigma_{ij}$ — тензор напряжений, $varepsilon _{{kl}},$ — тензор деформаций. Для изотропного материала тензор $C_{{ijkl}}$ содержит только два независимых коэффициента.

Благодаря симметрии тензоров напряжения и деформации, закон Гука может быть представлен в матричной форме.

Для линейно упругого изотропного тела:

varepsilon _{x}={frac {sigma _{x}}{E}}-{frac {mu }{E}}sigma _{y}-{frac {mu }{E}}sigma _{z}

varepsilon _{y}={frac {sigma _{y}}{E}}-{frac {mu }{E}}sigma _{x}-{frac {mu }{E}}sigma _{z}

varepsilon _{z}={frac {sigma _{z}}{E}}-{frac {mu }{E}}sigma _{x}-{frac {mu }{E}}sigma _{y}

gamma _{{xy}}={frac {tau _{{xy}}}{G}}

gamma _{{yz}}={frac {tau _{{yz}}}{G}}

gamma _{{xz}}={frac {tau _{{xz}}}{G}}

где $E$ — модуль Юнга, $mu$ — коэффициент Пуассона, $G={frac {E}{2(1+mu )}}$ — модуль сдвига.

Литература
Арнольд В. И. Гюйгенс и Барроу, Ньютон и Гук. М., Наука, 1989 г., 96 с.
Боголюбов А. Н. Гук Роберт // Математики. Механики. Биографический справочник. — Киев: Наукова думка, 1983. — 639 с.
Боголюбов А. Н. Роберт Гук (1635—1703) / Отв. ред. чл.-корр. АН УССР С. Н. Кожевников; Академия наук СССР. — М.: Наука, 1984. — 240 с. — (Научно-биографическая серия).
Родригес, Энрике Грасиан. В поисках формы. Гук. Закон Гука // Наука. Величайшие теории. — М.: Де Агостини, 2015. — Вып. 40. — ISSN 2409-0069.
Филонович С. Р. Роберт Гук. Квант, 1985, № 7.]
Филонович С. Р. Астрономия в творчестве Р.Гука // Историко-астрономические исследования.1986. Вып.18. С.259-290.
Храмов Ю. А. Гук Роберт // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — С. 94. — 400 с. — 200 000 экз. (в пер.)
Patterson L. D. Hooke’s Gravitation Theory and Its Influence on Newton. I: Hooke’s Gravitation Theory, Isis, Vol. 40, No. 4 (Nov., 1949), pp. 327—341.
Patterson L. D. Hooke’s Gravitation Theory and Its Influence on Newton. II: The Insufficiency of the Traditional Estimate, Isis, Vol. 41, No. 1 (Mar., 1950), pp. 32-45.
C. Wilson, Newton’s Orbit Problem: A Historian’s Response, The College Mathematics Journal, Vol. 25, No. 3 (May, 1994), pp. 193—200, doi:10.2307/2687647. Online
Early Science and Medicine, Volume 10, No. 4, December 2005. (недоступная ссылка) Выпуск журнала, содержащего ряд статей о вкладе Гука в теорию гравитации (авторы Niccolò Guicciardini, Michael Nauenberg, Ofer Gal, Domenico Bertoloni Meli).

Posted in Материаловедение,Строительные конструкции,Строительные материалы

Tagged with Закон Гука, Роберт Гук